定義は下記の2式のいずれかになります。
定義1
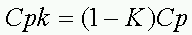
ただし
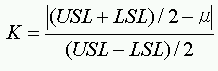
定義2
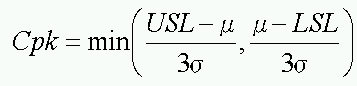 ただし min( ) は括弧内の最小値を返す関数とする。
ただし min( ) は括弧内の最小値を返す関数とする。2つも定義があるなんておかしな話ですが実は上記二つの定義はほぼ等しいです。
定義1を展開していくと....
Cpk =(1-K)*(USL-LSL)/6σ
=(1-[ABS{(USL + LSL) - 2μ} / (USL - LSL)] )*(USL-LSL)/6σ
=[{(USL-LSL)-ABS(USL+LSL-2μ)}/(USL-LSL)] * (USL-LSL)/6σ
={USL-LSL-ABS(USL+LSL-2μ)}/6σ
絶対値を展開します。
USL+LSL-2μ>=0 の時と USL+LSL-2μ<0 の時に分けて考えます。
(1)USL+LSL-2μ>=0 の時
Cpk =(USL-LSL-USL-LSL+2μ)/6σ
=(2μ-2LSL)/6σ
=(μ-LSL)/3σ
(2)USL+LSL-2μ<0 の時
Cpk =(USL-LSL+USL+LSL-2μ)/6σ
=(2USL-2μ)/6σ
=(USL-μ)/3σ
といった具合になります。
では絶対値を展開するときに使用した条件 USL+LSL-2μ>=0 とは具体的に何でしょうか? この式を変形させると下記のようになります
(USL+LSL)/2>=μ
これは規格中心と標本平均との比較に他なりません。
すなわち規格の中心に対して標本平均が小さければ下限規格との計算に、 大きければ上限規格との計算になるということです。
これは定義2のMIN関数での場合分けと合致します。