ここで、ある品物を作るケースにおいて、ある特性のばらつきが平均値μ(ミューと呼びます)、 標準偏差σの正規分布に従い、規格幅が(たまたま)6σである時のことを考えます。
このときCpは 6σ/6σ=1 です。
規格の中心と平均値が同じ場合、この状態は下図のようになります。
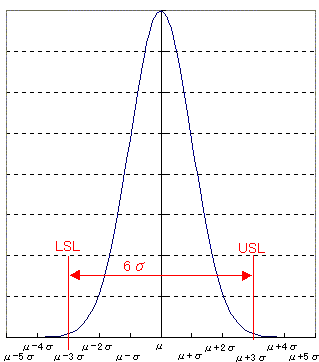
正規分布確率密度曲線において面積がその範囲の確率になりますので、今6σの範囲から 外れた両端の面積が規格外が発生する確率となります。
標準正規分布に変換し拡大した下図の黄色い面積(もちろん-∞からの面積)が下限側での
規格外発生確率となります。
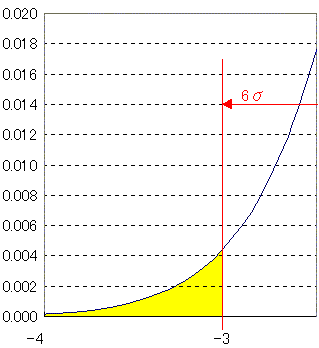
この面積pを計算すると約0.00135が求まります。
上限側も同じ面積なので、Cp=1の時の規格外発生確率は
p*2=0.00135*2=0.0027
となり約0.27%となります。
同様の方法で例えば規格幅が8σの時すなわちCp=8σ/6σ=1.3333…の時は
6.33*10-5
となり約63ppmとなります。
もう一つおまけで規格幅が10σの時すなわちCp=10σ/6σ=1.6666…の時は
5.74*10-7
となり約0.57ppmとなります。これは200万個ものを作って1個しか規格外れが
発生しないというきわめて優れた工程状態であるといえます。
※自分でこれを計算したいときは、EXCEL,OpenOffice.org/LibreOfficeのCalcともnormdist関数を使うと簡単に計算できます。
式は =normdist(x,0,1,true) で片側の面積が算出できますので、両側の場合はこれを2倍します。
なお、xのところに6シグマなら-3を、8シグマなら-4を入力します。